circ_make

概要

この関数は与えられた情報からQulacsで実行可能なBlock-Encodingを実行する回路を自動的に組み上げる

引数一覧

argument name	type	role
gate_inf	str	パウリ行列積の情報
zero_one	list(elements:int)	制御ビットの状態に関する情報
circ	QuantumCircuit(qulacs)	組み上げ先の回路
qubit	int	量子回路に必要な総ビット数
ancilla	int	量子回路に必要な補助ビット数

Python code

def circ_make(gate_inf, zero_one, circ, qubit, ancilla):
    """
    This function automatically constructs a quantum circuit for Qulacs that performs block encoding based on the given information.

    Parameters:
        gate_inf: the information of Pauli matrix product
        zero_one: the information of control qubits
        circ: a pre-defined quantum circuit used for actual computation
        qubit: the number of qubits which express the quantum state
        ancilla: the number of ancilla qubits for Block-Encoding

    Returns:
        None.
        A quantum circuit implementing Pauli operators with control qubits is created on circ.
    """
    # Local Values
    work_ope_order = [] # A list to store information about Pauli matrix product
    input_switch = 0 # A switch to initiate reading information about Pauli matrix product
    input_ele = "" # A temporary list to store information about Pauli matrix product
    # If Pauli matrix product is Identity,
    if gate_inf == "":
        gate_a = [[1., 0.],
                  [0., 1.]]
        for i in range(int(qubit - ancilla)):
            gate = DenseMatrix(int(ancilla + i), gate_a)
            mat_no = to_matrix_gate(gate)
            for j in range(len(zero_one)):
                cont_pos = len(zero_one) - j - 1
                mat_no.add_control_qubit(cont_pos, zero_one[j])
            circ.add_gate(mat_no)
    # If Pauli matrix product is the product of some Pauli matirces (ex: X0Y2Z4Y5)
    else:
        # Read the Pauli operators that make up the Pauli matrix product
        for i in range(len(gate_inf)):
            # Determine whether to interpret each item as a coefficient, a Pauli matrix product, or to ignore it.
            # 0: Read, 1: ignore
            if i < len(gate_inf) - 1.5:
                if input_switch > 0.3:
                    work_ope_order.append(input_ele)
                    input_ele = ""
                    input_switch = 0
                if gate_inf[i+1] == "X":
                    input_switch = 1
                if gate_inf[i+1] == "Y":
                    input_switch = 1
                if gate_inf[i+1] == "Z":
                    input_switch = 1
                if gate_inf[i+1] == "I":
                    input_switch = 1
                input_ele += gate_inf[i]
            else:
                work_ope_order.append(input_ele)
                input_switch = 0
                work_ope_order[-1] += gate_inf[-1]
        # Construct a quantum circuit from the reading results
        for i in range(len(work_ope_order)):
            num_inf = ""
            for j in range(len(work_ope_order[i])-1):
                num_inf += work_ope_order[i][j+1]
            tag_num = int(num_inf)
            gate_pos = qubit - tag_num - 1
            if work_ope_order[i][0] == "X":
                gate_a = X(gate_pos)
                mat_no = to_matrix_gate(gate_a)
                for j in range(len(zero_one)):
                    cont_pos = len(zero_one) - j - 1
                    mat_no.add_control_qubit(cont_pos,
                                             zero_one[j])
            elif work_ope_order[i][0] == "Y":
                gate_a = Y(gate_pos)
                mat_no = to_matrix_gate(gate_a)
                for j in range(len(zero_one)):
                    cont_pos = len(zero_one) - j - 1
                    mat_no.add_control_qubit(cont_pos,
                                             zero_one[j])
            elif work_ope_order[i][0] == "Z":
                gate_a = Z(gate_pos)
                mat_no = to_matrix_gate(gate_a)
                for j in range(len(zero_one)):
                    cont_pos = len(zero_one) - j - 1
                    mat_no.add_control_qubit(cont_pos,
                                             zero_one[j])
            elif work_ope_order[i][0] == "I":
                gate_a = [[1, 0],
                          [0, 1]]
                gate = DenseMatrix(int(gate_inf[2*i+1]), gate_a)
                mat_no = to_matrix_gate(gate)
                for j in range(len(zero_one)):
                    cont_pos = len(zero_one) - j - 1
                    mat_no.add_control_qubit(cont_pos,
                                             zero_one[j])
            circ.add_gate(mat_no)

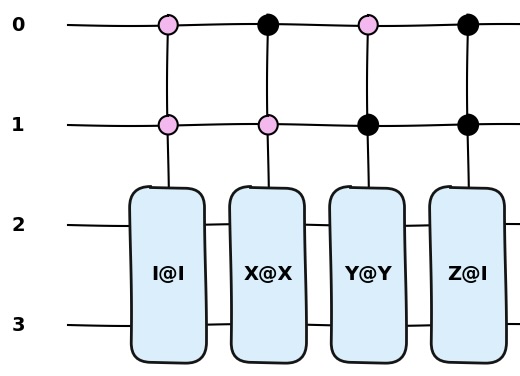
実行例

import numpy as np
import pitbe
from qulacs import QuantumState, QuantumCircuit
from qulacs.gate import X, Y, Z, DenseMatrix, to_matrix_gate

circuit = QuantumCircuit(4)
ope_lst = ["I0I1", "X0X1", "Y0Y1", "Z0I1"]
cont_list = [[0, 0], [1, 0],
             [0, 1], [1, 1]]

for j in range(len(cont_list)):
    pitbe.circ_make(ope_lst[j], cont_list[j], circuit, 4, 2)

作成された回路図

注意点

前述の通りこの関数には「qulacs」のクラスを一部用いているので 必ず関数のimport部分で「qulacs」をimportすること

また引数「zero_list」の値に説明時に触れたもの以外を 代入した場合想定外の挙動をとる場合もある